Ancient Indian mathematics is a remarkable chapter in the history of human knowledge, characterized by its originality, depth, and lasting impact on global mathematical thought. Synonymous with the rich tradition of Vedic Mathematics, this ancient discipline highlights the profound intellectual achievements of India, deeply intertwined with its spiritual and cultural heritage. The foundation of this mathematical tradition lies in the Vedas, especially through their ancillary texts—the Vedangas—among which Jyotisha holds particular significance as the science of astronomy and mathematics. This essay endeavors to explore the multifaceted contributions of ancient Indian mathematics, emphasizing its origins in Vedic literature, the evolution of key mathematical concepts, and the eminent scholars who propelled this tradition forward.
At the heart of ancient Indian mathematics are the powerful tools known as the 16 Sutras and 16 Upasutras of Vedic Mathematics. These concise aphorisms, or formulaic rules, served as mnemonic devices enabling scholars to solve highly complex mathematical problems mentally and with remarkable speed. The sheer elegance and utility of these sutras underscore the depth of mathematical understanding present in Vedic times. Just as Hinduism’s roots are entrenched in the Vedas, so too is the mathematical tradition firmly grounded in these ancient texts, which reveal an early synthesis of ritualistic practice and scientific inquiry.
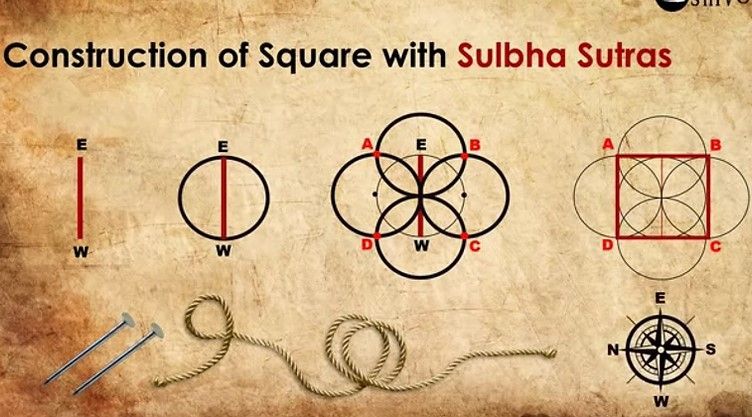
One of the earliest and most profound connections between Indian mathematics and its cultural practices can be observed in the construction of fire altars, described in texts such as the Śulbasūtras attributed to Baudhayana, Apastamba, and Katyayana. These works, dated around 800 BCE though reflective of much older oral traditions, are among the first systematic treatises on geometry and arithmetic. The Śulbasūtras belong to the late Vedic period and represent mathematical knowledge applied in ritual contexts. Remarkably, these texts present an explicit statement of what is now known as the Pythagorean theorem, well before its formal recognition in Greek geometry. The geometric constructions necessary for precise altar building led to a tradition of mathematical rigor and visualization that informed later developments.
The pragmatic need to memorize and transmit complex knowledge across generations without relying on perishable written scripts shaped the ancient Indian mathematical tradition. Mathematical knowledge was composed in terse, metrical verses, enhancing memorability and ensuring its preservation through oral tradition. This mode of transmission reflects the broader pedagogical culture of the Vedic period, where oral memorization was paramount for safeguarding sacred and scientific knowledge alike.
Beyond geometry, ancient Indian mathematics made pioneering contributions to arithmetic and algebra. The concepts of the decimal system and the place value notation, including the revolutionary notion of zero as a digit, originated in the Indian subcontinent. This decimal notation not only simplified calculations but also played a crucial role in fostering the growth of trade and commerce, by providing a standardized numerical framework conducive to large-scale economic activities. Moreover, the decimal system catalyzed advancements in astronomy and other sciences, positioning India’s mathematical tradition as a cornerstone for modern civilization.
The progression of algebra as a distinct mathematical discipline is evident by the time of eminent mathematicians such as Aryabhata (476–550 CE) and Brahmagupta (598–670 CE). Aryabhata’s works include sophisticated algorithms and methods for solving quadratic equations, while Brahmagupta introduced rules for arithmetic involving zero and negative numbers, and articulated solutions to various algebraic problems. Their contributions mark a significant evolution from earlier geometric and arithmetic traditions to a more abstract and symbolic mathematical discourse.
In geometry, as well as trigonometry and calculus, ancient Indian scholars exhibited profound expertise. The tradition of trigonometry, essential for astronomical calculations, was highly refined by Madhava of Sangamagrama (circa 1340–1425 CE), who laid the groundwork for infinite series expansions—a precursor to calculus. This tradition flourished well before similar ideas emerged in Europe, demonstrating the advanced mathematical thinking present in India.
The symbiosis between astronomy and mathematics in ancient India is exemplified by mathematician-astronomers such as Bhaskara I, Brahmagupta, and later Bhaskara II. Their works seamlessly integrated observational data with mathematical innovation, reflecting a holistic approach that linked empirical investigation with theoretical advancement. These scholars produced comprehensive treatises that addressed complex problems in planetary motion, eclipses, and time-keeping, employing methods that required deep mathematical insight.
In conclusion, ancient Indian mathematics reveals a civilization deeply engaged in intellectual pursuits that melded sacred traditions with scientific rigor. From the concise and potent sutras of the Vedas, through the ritualistic geometry of the Śulbasūtras, to the revolutionary decimal system and sophisticated algebraic and trigonometric frameworks, Indian mathematicians made profound contributions that shaped the trajectory of global mathematics. Their legacy is not only a testament to their ingenuity but also an enduring foundation that continues to influence and inspire contemporary mathematical thought worldwide.